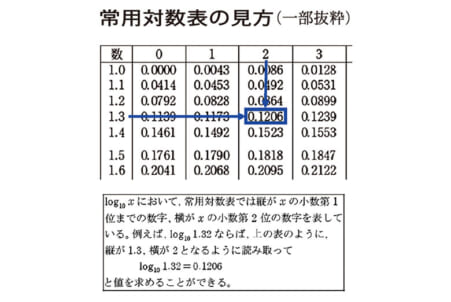
新課程、思考力重視は継続
数学

　令和７年度大学入学共通テストは、新課程初年度の実施となった。数学Ⅰ・Aは、試験時間７０分で変更はなかったが、大問構成は大きく変わった。従来の必答２題、選択２題（３題中）の計４題から、全問必答の４題に変更された。
　一方、数学Ⅱ・B・Cは、旧課程の数学Ⅱ・Bから試験時間が１０分延長され７０分となった。大問も必答２題、選択２題（３題中）の計４題から、必答３題、選択３題（４題中）の計６題へと増えている。
　新課程の内容としては、数学Ⅰ・Aで「データの分析」の外れ値や仮説検定、そして「場合の数と確率」の期待値に関する問題が登場した。また、数学Ⅱ・B・Cからは「統計的な推測」の仮説検定、さらに「平面上の曲線と複素数平面」の複素数平面に関する問題が出題された。
　共通テストは５年目を迎えたが、数学の基礎・基本を問う形に加え、状況を把握する力や、状態変化への対応を問う思考力重視の問題は、丁寧な誘導の下で継続的に見られる。
　数学I・Aの第４問「場合の数と確率」では、期待値の問題が出された。期待値自体は平成２５年以前のセンター試験でも扱われていたが、共通テストでは期待値の大小から判断の妥当性や損得などを考慮する要素が加わっている。なお、この問題では期待値を考える上で有用な表が問題文中に与えられている。７０分という限られた時間の中で、こうしたヒントをいかに活用できるかも得点するためのカギとなる。
　また、数学Ⅱ・B・Cの第２問「指数関数・対数関数」では、常用対数表を利用する問題が本試で初めて出題された。受験生は、真数が与えられたときの常用対数の値、そして常用対数の値が与えられた場合の真数の値の双方を求められるように準備しておく必要がある。常用対数表以外にも、三角比・三角関数の表、正規分布表なども正しく読み取れるようにしておきたい。
　共通テストでは、授業や日常生活の場面を題材にした問題が多く出されるため、表面的な情報に目がいきがちである。しかし、あくまで内容は「数学」であるため、まずは教科書などで基礎・基本を確実に固めておくことが重要となる。
　ただし、問題の解き方を暗記するような方法では、高得点を取ることは難しい。日頃の学習で

　（１）各分野の導入となる考え方を大事にする
　（２）別解を含めたさまざまな解法を身に付ける
　（３）計算練習を含むアウトプットをしっかりと行う

　―ことを意識して実行してほしい。並行して、苦手分野の徹底補完や、問題文から必要な情報を読み取る読解力の養成、７０分という時間を意識した演習を行うとよいだろう。対策を戦略的に進めるためにも、過去問や共通テスト型の模試を積極的に活用することをお勧めする。
　（東進ハイスクール・東進衛星予備校　数学科）